[閒聊] 理科生的廁所花子
https://x.com/man_Arihred/status/1732342140620116346?s=20
https://pbs.twimg.com/media/GAqD2yTacAAqaoZ.jpg
【晚上的學校三樓】
「來觀察蟲子的不小心看到這麼晚了」
「上個廁所就回去吧...」
【明明空無一人的女生廁所】
【在第O間的門內】
https://pbs.twimg.com/media/GAqECbTaYAAdI-1.jpg
【有理組的花子在】
【似乎看到了就會被帶去那邊的世界】
https://pbs.twimg.com/media/GAqEC4PaEAAmo4V.jpg
「怎...怎麼辦 如果真的有花子在的話...」
「確實是在三樓的女廁...但第幾扇門...忘了...」
「如果不小心開到的話......」
「機率是三分之一嗎...」
(我要冷靜點...怎麼可能有花子在啊...)
(準備打開第二扇門)
https://pbs.twimg.com/media/GAqED0gaoAEDuxi.jpg
(第一扇門突然發出聲響)
「門是鎖起來的...旁邊有誰在嗎...？」
(改去第一扇門)
「...花子...請問妳在嗎...？」
https://pbs.twimg.com/media/GAqEEbRbUAAPUF0.jpg
「 在 」
(！？)
(不在這扇門內...聲音是從左邊傳來的...)
(但到底是第二間還是第三間.....)
「怎麼辦...變二分之一了...)
「有一間裡有花子...如果打開的話...」
https://pbs.twimg.com/media/GAqEKRcaMAAk1u3.jpg
「不對...不是二分之一 這是...蒙提霍爾問題！」
蒙提霍爾問題(山羊問題、三門問題)
少女選了其中一扇門
接著花子把自己不在的剩下那間門給鎖起來
接著重選 門裡有花子在的機率乍一看是二分之一
https://pbs.twimg.com/media/GAqEKtjacAA-eo4.jpg
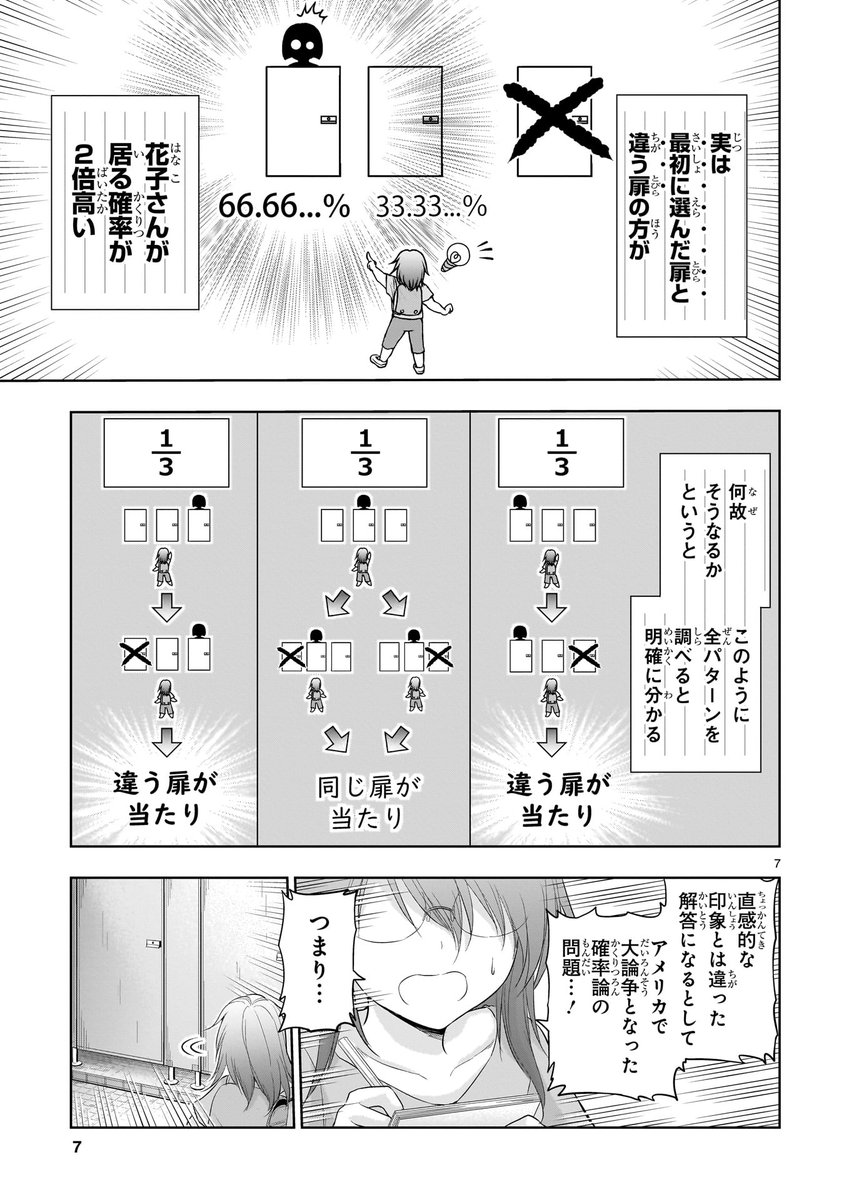
但其實不然 其實選跟最開始那扇不同的門
裡面有花子的機率竟有兩倍之高
為什麼呢
像這樣把全部的路線畫出來就很明瞭了
「這是答案很反直覺 在美國也引起廣大爭論的機率問題...！」
「所以說...！」
https://pbs.twimg.com/media/GAqELGqbIAAJWMl.jpg
「花子在第三間裡面！」
「果然沒錯~！這是蒙提霍爾問題的重現對吧」
「能明白這個梗的人妳還是第一個呢...」
「果然是呢~！」
https://pbs.twimg.com/media/GAqELmebwAA1rjN.jpg
然後少女跟花子
兩人因興趣相投 互相理解了
「這題真有趣呢 妳也喜歡數學嗎？」
「嗯...接著來討論柯尼斯堡七橋問題吧」
「來吧來吧」
就這樣 兩人不斷的討論直到三更半夜——
「...以前 好像有過這樣的事 但那是現實嗎 還是夢呢...」
(現實才不可能那種事發生吧)
.
.
.
看到三選一
腦袋就浮現了三門問題 也是很經典的題目呢
想起來以前大學在補習班打工的時候
看到國中生的考卷竟然出了這題還讓我驚訝了一下
是說這題第一次見的話
國中國小根本寫不出來吧
太反直覺了
--
考試時間夠有筆的話，就是樹狀圖開下去
長大後也變得太多了吧...
碰到這類問題就放大規模來看 1000個門鎖上998個
花子還拿數學課本www
不過選對的機率只有三分之二，在只有一次選擇機會下其實
還是很可能失敗的XD
太可怕了 是三門問題
笑死
這世界的鬼怪都特別好學，之前那個筆仙也很扯XD
這花子是理科的呢
裂嘴女那個好像就普通被撩而已?
有梗XD
看了這篇才知道 超神奇 很違反直覺
筆仙是被強迫的吧XDDD
畢竟學力等同戰鬥力的世界觀 需要吧w
花子在左邊：她只能鎖最右邊的門，100%符合實際條件
花子在中間：她可以鎖左或右邊的門，50%符合實際條件
所以花子在左邊的機率是在中間的兩倍
這是不畫圖時比較勉強能解釋的一種說法，但還是很抽象
簡單來說只有一開始就選中1/3的花子才能換門避開，2/3共
菇的你換門就是遇到花子
筆仙救我高微
可以請筆仙計算Σ(-1)^n的級數極限是多少
然後就可以發明簡易版的永動機
拜託給我修女
喔 貝氏統計
三門問題 我記得八卦版有一篇討論超長
那個花子也太獵奇......
花子：聊到忘記賺業績了 失敗
笑死XD
聊著聊著都能順便超渡了吧
XDDD
是什麼21點電影裡面那個嗎？
花子跟筆仙強強聯手 人類科技應該可以快進一百年
63
Re: [討論] 完全不能接受有智商大於200的人設推 LeonBolton : 大家似乎都忽略了一點，如果真有智商197才能解的謎 08/04 01:54 → LeonBolton : 題，就算作者寫得出來，讀者就一定看得懂？ 08/04 01:54 你說的這個有個經典例子，也是經典數學題。 那就是有名的三門問題。![Re: [討論] 完全不能接受有智商大於200的人設](https://i.imgur.com/rnBkIvIb.jpg "Re: [討論] 完全不能接受有智商大於200的人設")
35
[蔚藍] 泳裝花子個人劇情 (雷)小春推牆壁防雷 劇情1![[蔚藍] 泳裝花子個人劇情 (雷)](https://i.imgur.com/63rPsEdb.jpg "[蔚藍] 泳裝花子個人劇情 (雷)")
22
[閒聊] 廁所的花子竟然是個一零九辣妹要怎麼辦？那一天上班想去廁所拉屎摸魚 見鬼啦～嘿嘿～ 原來是大名鼎鼎的廁所花子![[閒聊] 廁所的花子竟然是個一零九辣妹要怎麼辦？](https://i.imgur.com/tCZdFSvb.jpg "[閒聊] 廁所的花子竟然是個一零九辣妹要怎麼辦？")
17
[問卦] 廁所裏的花子的八卦？截自維基百科： 廁所裏的花子（日語：トイレの花子さん／トイレのはなこさん Toire no hanakosan） ，即相傳在學校廁所出沒的幽靈少女，是日本的都市傳說。 這則故事有著不同版本——一說認為花子是二戰時期的學生，在捉迷藏時不幸死於空襲； 另有一說認為她在學校被父母或陌生人殺害；此外亦有說法指花子是在學校自殺。![[問卦] 廁所裏的花子的八卦？](https://i.imgur.com/FWGFT0zb.jpg "[問卦] 廁所裏的花子的八卦？")
14
Re: [問卦] 三扇門的問題 33.3% or 50%我們這邊先不討論蒙提霍爾問題 先來討論一下擲骰子 假設有一均質正六面體骰子 將數字1~6分別刻在6個面上 那假設你擲出這個骰子一次 假設是數字1朝上好了 那你應該能接受骰出1的機率是1/6吧?11
[閒聊] 西瓜妹妹 12 廁所花子森とんかつ《スイカ》 01、02：#1VN9KZcr (C_Chat) #12 男生站小便斗通常都會隔一個![[閒聊] 西瓜妹妹 12 廁所花子](https://i.imgur.com/vxjGlVgb.jpg "[閒聊] 西瓜妹妹 12 廁所花子")
5
[問卦] 怎麼最近一堆人刷花子 花子是誰看到這兩天一堆人在那邊刷花子，完全不知道是啥 花子不是日本那個待在廁所的鬼嗎 還是有其他的東西，有沒有八卦 --![[問卦] 怎麼最近一堆人刷花子 花子是誰](https://i.imgur.com/zpuXCLMb.jpg "[問卦] 怎麼最近一堆人刷花子 花子是誰")
7
[問卦] 花子為什麼要欸欸 如題 日本鄉野傳說 花子 相傳會在學校廁所幫你擦屁股7
[閒聊] 叫我要走正規程序阿-怪異さんと俺- 「正しい手順で呼びなさい」 （1/2） #イラスト![[閒聊] 叫我要走正規程序阿](https://pbs.twimg.com/media/F8Kb-uIbIAAFDLs.jpg "[閒聊] 叫我要走正規程序阿")
5
[問卦] 廁所的花子被偷看會害怕嗎?日本學校怪談很經典的廁所的花子 有著各種不同的傳說 例如會找你一起在廁所一起玩 或是喊著門打不開之類 如果現在有台灣中年大叔 爬上門看著花子 害怕的會是花子還是中年大叔呢?![[問卦] 廁所的花子被偷看會害怕嗎?](https://i.imgur.com/aCcCOY0b.jpg "[問卦] 廁所的花子被偷看會害怕嗎?")
24
[閒聊] 寫作業求助谷歌AI！美國學生被嗆去死驚呆![[閒聊] 寫作業求助谷歌AI！美國學生被嗆去死驚呆](https://img.youtube.com/vi/BBFovNPMIEc/mqdefault.jpg "[閒聊] 寫作業求助谷歌AI！美國學生被嗆去死驚呆")
44
[閒聊] 現代作家編劇能力真沒比較差嗎？爆
Re: [日劇] 戀上換裝娃娃 夢魔莉茲的COS![Re: [日劇] 戀上換裝娃娃 夢魔莉茲的COS](https://i.imgur.com/EYYeABPb.jpeg "Re: [日劇] 戀上換裝娃娃 夢魔莉茲的COS")
23
[死神] 京樂帶那些雜魚幹嘛？![[死神] 京樂帶那些雜魚幹嘛？](https://i.imgur.com/U8Ejehhb.jpg "[死神] 京樂帶那些雜魚幹嘛？")
19
[24秋] 魔王2099 06![[24秋] 魔王2099 06](https://i.imgur.com/LEGjkbMb.png "[24秋] 魔王2099 06")
18
[少前2] 少女前線2封測心得![[少前2] 少女前線2封測心得](https://i.imgur.com/t4E2Lyzb.jpeg "[少前2] 少女前線2封測心得")
82
[閒聊] 在日本街上遇到了超壯的黑人![[閒聊] 在日本街上遇到了超壯的黑人](https://pbs.twimg.com/media/GcayHt1bEAAfbZ1.jpg "[閒聊] 在日本街上遇到了超壯的黑人")
15
[閒聊] 快要輸的瑪莉蘿絲![[閒聊] 快要輸的瑪莉蘿絲](https://i.imgur.com/EHPJjZIb.png "[閒聊] 快要輸的瑪莉蘿絲")
14
[24秋] 藍色監獄二期 31 太神啦凪72
Re: [索尼] 社長：承認星鳴失敗，已得教訓、應更12
Re: [閒聊] 看了中國毒物反而看不下日本毒物19
Re: [日劇] 戀上換裝娃娃 夢魔莉茲的COS![Re: [日劇] 戀上換裝娃娃 夢魔莉茲的COS](https://i.imgur.com/RMTKhc1b.jpeg "Re: [日劇] 戀上換裝娃娃 夢魔莉茲的COS")
11
[討論] 如果那個闇龍紀元的牛頭人59
[MYGO] 看了第一話 這在演甚麼怪東西?![[MYGO] 看了第一話 這在演甚麼怪東西?](https://i.imgur.com/UKjXRAeb.jpeg "[MYGO] 看了第一話 這在演甚麼怪東西?")
爆
[閒聊] K 社新的一番賞真的很會 (已發)12
Re: [討論] PTCG 活動45勝心得![Re: [討論] PTCG 活動45勝心得](https://i.imgur.com/tfiVaODb.jpg "Re: [討論] PTCG 活動45勝心得")
43
[閒聊] 膽大黨裂嘴女有那麼強？![[閒聊] 膽大黨裂嘴女有那麼強？](https://i.imgur.com/AJFgzY8b.jpeg "[閒聊] 膽大黨裂嘴女有那麼強？")
8
[閒聊] 我死神這集怎麼一直停在這個地方啊？![[閒聊] 我死神這集怎麼一直停在這個地方啊？](https://i.imgur.com/r4Da00Pb.gif "[閒聊] 我死神這集怎麼一直停在這個地方啊？")
29
[情報] 死神 千年血戰篇-相剋譚 07![[情報] 死神 千年血戰篇-相剋譚 07](https://i.imgur.com/pkiFq2hb.png "[情報] 死神 千年血戰篇-相剋譚 07")
7
[Vtub] 哈洽馬最近的路線是養生嗎？![[Vtub] 哈洽馬最近的路線是養生嗎？](https://pbs.twimg.com/media/GW0kdsvWMAA_tcO.jpg "[Vtub] 哈洽馬最近的路線是養生嗎？")
7
[問題] NICONICO 是完全鎖國了嗎?![[問題] NICONICO 是完全鎖國了嗎?](https://i.imgur.com/S8k32GUb.jpg "[問題] NICONICO 是完全鎖國了嗎?")
11
[蔚藍] 秋服阿葵![[蔚藍] 秋服阿葵](https://i.imgur.com/mwGB6SUb.jpeg "[蔚藍] 秋服阿葵")
24
[問題] 黑傑克賠最多的是哪一個病例?6
Re: [閒聊] 地雷系有什麼特色？![Re: [閒聊] 地雷系有什麼特色？](https://i.imgur.com/BoEpLtrb.jpg "Re: [閒聊] 地雷系有什麼特色？")
6
[閒聊] 甘神二女沒在穿奶罩嗎![[閒聊] 甘神二女沒在穿奶罩嗎](https://i.imgur.com/DSQamcOb.jpeg "[閒聊] 甘神二女沒在穿奶罩嗎")
5
[閒聊] 奧術是不是跌落神壇了?![[閒聊] 奧術是不是跌落神壇了?](https://i.imgur.com/UUmNy8ub.jpg "[閒聊] 奧術是不是跌落神壇了?")
23
[閒聊] 二創很有名的作品有哪些？11
[24秋] 2.5次元的誘惑 20 太扯了![[24秋] 2.5次元的誘惑 20 太扯了](https://i.imgur.com/nF5zrn9b.png "[24秋] 2.5次元的誘惑 20 太扯了")
5
Re: [情報] 「結束バンド」Oricon Weekly Ranking23
Re: [閒聊] 東立連齊木楠雄都可以斷尾喔![Re: [閒聊] 東立連齊木楠雄都可以斷尾喔](https://imgpoi.com/i/XAF7MD.jpg "Re: [閒聊] 東立連齊木楠雄都可以斷尾喔")