Re: [問題] 無限多的自然數跟質數誰比較多？
直接說結論: 一樣多
姑且身為一個有靠數學招搖撞騙的小廢廢 應該可以提供個簡單的解答
但我知道西洽存在112數學系拿卷畢業 然後現在應該在國外讀博的版友
偶而也有112數學系畢業 然後讀電機碩的版友
相比之下我就只是個廢物Q_Q
關於自然數與質數誰比較多 這個驗證方式應該分為兩個步驟
1.質數是否為無限多個?
2.若質數為無限多個 那質數與自然數如何比較?
首先1.
質數有無限多個。
其證明方式非常簡單 用最基本的反證法即可
因"質數有無限多個"與"質數為有限多個"為相反的命題
故先假設"質數為有限多個"
則我們可以從小到大 將所有質數編號 p_1,p_2,p_3......p_n p_n為最大的質數
而若我們寫出一個大數N為所有質數的乘積
則會發現N+1不能被以上所有的質數給整除(餘數皆為1)
那麼就可以得出N+1亦為一個質數 且比p_n還要大 與最初的命題矛盾
所以可以得知"質數有無限多個" Q.E.D
再來2.
無限多個的自然數 與 無限多個的質數 其數量一樣多
非常簡單
我們可以說
"第一個"自然數為1 "第一個"質數為2
"第二個"自然數為2 "第二個"質數為3
"第三個"自然數為3 "第三個"質數為5
......
以此類推
所有"第N個"自然數都可以對應到一個數 同時"第N個"質數亦可對應到一個數
那麼儘管有點違反直覺 但實際上論"個數" 則自然數的個數與質數的個數是一樣多的
或者說 只要能找到任何一個無法同時存在有"第M個"自然數 但沒有"第M個"質數的狀況
就能說自然數的個數 與 質數的個數不相同
這種概念在所有的"可數集合"均成立
進階一點就像"有理數的的個數"也與"正整數的個數"是一樣多的
但是當命題拉到不是可數集合的時候 就不會那麼簡單了
就像無理數的個數有無限多個 正整數的個數也有無限多個
但無理數的個數卻是遠大於正整數的個數
不過要去說明就懶了 大概也沒人在乎
數學嘛 就是這麼反直覺 唉
--
https://imgur.com/r8P0qbu.jpg
--
「無理數的數量跟有理數的數量中間有沒有別的無限」
對於那些主張正解應該是無法比較而不是一樣多的有何看法
請他們找個數學老師問。
這個問題的結論好像也是讓數學界很頭大
你很厲害www
你好認真
趕快推不然被人發現我看不懂
跟文組解釋那麼多幹嘛==
每次都覺得數學才是真正的玄學==
我不能只會微積分跟傅立葉變換就好了嗎：（
質數無限多個這個高中就有證了
至於要證質數和自然數一樣多可沒有這麼簡單
要找到bijection
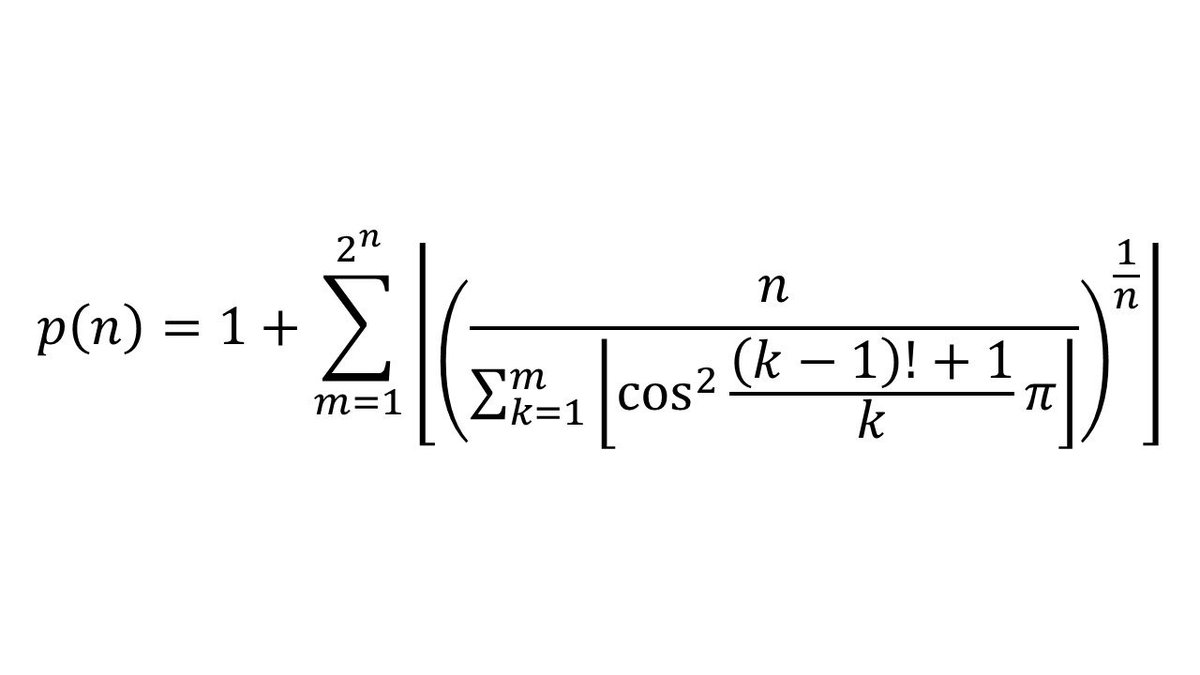
代自然數n進去會生出第n個質數的謎公式
想起以前考資工所離散數學的數論 真的不知道在供三小
嗯嗯 跟我想的一樣
推個
那什麼神祕公式啦 XDDDD
另外一個比容易的方法，就是找兩個1-1函數
證這個不需要用複雜的公式啊 只要有演算法算出第N個質數就
好了 有人問為何是bijection就說是一個一個數的
另外一樓說的是連續統假設 在ZFC內無法證明也無法證否
樓上你不要再加新名詞了 到時候有人好奇ZFC是什麼XD
x=0
講的不錯 易懂
因為質數是自然數子集，一邊的1-1很容易
另外一邊就用Well-ordering principle可以做出來
好 我問 ZFC是什麼
講中文啦 乾
ZFC就是現在數學最常用的公理系統
那有KFC嗎？
ZFC的概念就是把早期數學中發現的重要邏輯矛盾補起來
有人會問公理系統是什麼
推，寫的蠻好懂的
都在算第一個質數、第二個質數了，這不是bijection什麼才是
推推文
不是，證明不能直接說第一個第二個，因為說第一個第二
個隱含的意思就是你找到一個函數對應自然數和質數
你要真的把拿個函數做出來才是證明
我是覺得啦 除非是本科系的 不然越講越細節只會讓大家越來越排斥數學 唉 數學其實很有趣的
(指指我po的圖)
如果是找一對反函數 函數用演算法的形式寫出呢
我以為不能直接用第1、2、3個來證明，而是要證明一一
對應的關係才能知道他們是一樣多？例如自然數跟偶數一
樣多可以符合n與2n，有幾個自然數就有幾個偶數這樣
科普向的就別要求那麼多了 你要我全部完整寫出來就也沒人要看了(實話是我也懶得寫)
雖然是不懂數學但看一些科普書真的覺得數學就是魔法
就算喜歡數學也不見得會想要自己跳下去完整解題老實講XD
有一個旅館 每個房間都有一個不重複的自然數編號 今天
來了一群客人 每位客人都有一個質數編號 每位客人都
要住進字面上等同自己編號的房間 所有客人check in 完
成後 空房間是無限的嗎？有住人的房間是否遠少於沒住
人的房間？
（客人的質數編號也相互不重複）
謝謝你希爾伯特
淺顯易懂
所有質數的乘積+1 不一定是質數吧?
這邊要先注意到前提 是"質數為有限多個" 而這個乘積+1 除以 任何一個質數均是餘一 其他所有的合數也可以視為質數的乘積(可以質因數分解) 從定義上 這一個數的正因數僅有"1"與"自己"時 就是個質數 那這個N+1就會是個質數
※ 編輯: zax8419 (116.89.129.129 臺灣), 05/16/2023 20:19:30有無限的房間卻常常客滿的飯店
0..0
假設有n個質數 1.其實還有第n+1個質數可以整除N+1 2.N+
1是質數
謝謝你數學人 看到推文那個公式有個cos我更不懂了
感謝科普
我把標題改寫一下 應該就能讓人懂了吧
1000個自然數跟 1000個質數 誰比較多???
五公斤的棉花 跟五公斤的鐵塊 誰比較重
※ 編輯: zax8419 (116.89.129.129 臺灣), 05/16/2023 20:32:33推個 以前修過數學系的數學導論，後來就聳了...
是說ZFC好像是集合論會帶到的東西?
其實反證法這東西即使是理工科的人也有不小比例搞不懂…
黃子嘉有教過
1樓說的那個東西是戴德金分割，已經有證明了
樓上你再看清楚一點我寫的東西是什麼XD
你好棒
Dedekind cut是講實數完備性
跟不連續統假設是兩件事
講的很有道理 對吧發仔
以中學數學來說，你寫的很棒，好懂又沒省略太多
嗯嗯 就是這樣
寫得蠻好理解的耶
推
OKOK 懂了 永遠都有更大的質數所以是無限多個質數這樣
文章看太快
那個公式也太鬼了
好懷念 是我高中的東西
這我也會 第一題 trivial 第二題我會但是推文寫不下
專業
不是我不在乎 是我看不太懂 我知道你講中文 但是合在一起
像外星人講話
數學系 覺得這篇講的滿淺白的 以科普的角度來看其實不
錯
我剛剛還以為我在八卦 特地看作者是不是張阿月
雖然跟主題沒什麼關係，不過QED的D後面要加點喔，它跟
RIP的P一樣很容易被忘記
73
首Po在無限多的情況下 自然數跟質數誰比較多呢？ 玩星穹鐵道出的任務 感覺上每多出一個質數 就會多出好多的自然數![[問題] 無限多的自然數跟質數誰比較多？](https://img.youtube.com/vi/RJS3Z2DYEO4/mqdefault.jpg "[問題] 無限多的自然數跟質數誰比較多？")
18
那個不好意思借串問一下 我朋友之前跟我說這台車不會動 但我一直聽不太懂 所以請問為什麼不會…![Re: [問題] 無限多的自然數跟質數誰比較多？](https://i.imgur.com/AVRvFFeb.jpg "Re: [問題] 無限多的自然數跟質數誰比較多？")
51
其實你第一個證明有點瑕疵 令 N = 1 + p_1*p_2*...*p_k的作法 我能舉個反例： 1 + 2*3*5*7*11*13 = 30031 = 59*509 此時N可以表達成兩個不為{1,N}元素的自然數之乘積27
其實這個想法要寫的嚴謹一點還有點意思 你已經做出 "排序"這件事了 當然這裡很明顯的用大小來做排序了 其實已經用到 最小上界存在![Re: [問題] 無限多的自然數跟質數誰比較多？](https://i.imgur.com/eAa4UOIb.jpg "Re: [問題] 無限多的自然數跟質數誰比較多？")
25
「答案是一樣多」 你不見得要接受這講法啊 用 N 和 P 來分別代表 自然數 和 質數，大家會發現： (1) P 有的數，N都有 (2) 有些數，只有N有，P沒有 在這個認知下，覺得「一樣多」很奇怪沒啥問題![Re: [問題] 無限多的自然數跟質數誰比較多？](https://img.youtube.com/vi/b8cSITGGzEw/mqdefault.jpg "Re: [問題] 無限多的自然數跟質數誰比較多？")
9
突然想到一個東西 雖然跟原文無關 不過也算離散數學的範圍 就是有沒有人也覺得鴿籠原理很屌 很白痴的原理 十隻鴿子要放進九個籠子裡 一定至少一個籠子有兩隻鴿子 一開始覺得 幹這什麼廢物原理 小學生都會 不過當他開始在一些意想不到或是莫名其妙的地方跑出來的時候（通常是證明）我就覺得 靠這東西真的太屌了 比如說有限狀態機、6個人之中必有3個人互相認識或互相不認識之類的 常常就覺得 幹 又有鴿籠 還有遞迴的概念 我不用知道怎麼做 我只要知道做完的結果和上一步的關係是什麼就可以解了 真的有種重新認識這世界的感覺10
推 hutao: 做個每日還這麼哈扣，不曉得以後會不會來0.999_=1 05/17 00:35 來開個新主題 0.9bar = 1 ? 直接講結論: 是對的 也不是對的 至於如何"說明"(這邊先不用"證明"一詞)![Re: [問題] 無限多的自然數跟質數誰比較多？](https://i.imgur.com/YgqfJKtb.jpg "Re: [問題] 無限多的自然數跟質數誰比較多？")
對小學生來說這個有點困難，因為小學生普遍沒什麼代數的概念 我比較建議擱置這問題。 : 二、如果是對國中生說 : 三、如果是對高中生說 : 0.9bar = 0.9 + 0.09 + 0.009 + 0.0009 + ......![Re: [問題] 無限多的自然數跟質數誰比較多？](https://img.youtube.com/vi/l6rlIOetkwg/mqdefault.jpg "Re: [問題] 無限多的自然數跟質數誰比較多？")
2
: : 0.9bar = lim An : n->∞ : 基於上面的描述，會得到 0.9bar = 1 : 不同意的，就叫他自己描述一下他心中的 0.9bar 是什麼樣子15
雖然這是學術論壇 但到底為啥在C_CHAT寫證明呢... 然後為啥我要點進來看呢? 看了讓我想回文 也很神祕 ※ 引述《yueayase (scrya)》之銘言：
爆
[問卦] 7777777是介於6跟8之間的自然數 也是第4個質數 前一個是5 下一個是11 啊有沒有7的八卦 o'_'o?![[問卦] 777777](https://i.imgur.com/GQWJAT8b.jpg "[問卦] 777777")
10
[問卦] 數質數真的能讓人冷靜嗎？我認識一位神父 之前跟他聊天的時候提到說 如果遇到緊急狀況 他都用數質數來緩和情緒 過一陣子我遇到了臨時狀況8
[問卦] 質數跟自然數誰比較多啊？安安大家好我文組 在隔壁版看到這題 自然數總共無限個 質數也有無限多個 在有限的範圍裏面 理論上質數比較少 但如果拉到整體看 全部的數量比起來 哪一個會比較多呢 有人說無限不能比![[問卦] 質數跟自然數誰比較多啊？](https://i.imgur.com/WIhyfdKb.jpg "[問卦] 質數跟自然數誰比較多啊？")
6
[問卦] 振興券用質數來命名？安安 欸 幹 我發現一個恐怖巧合 就是歷來振興券都是質數 3倍券=3質數 5倍券=5質數![[問卦] 振興券用質數來命名？](https://i.imgur.com/DlsavnBb.jpg "[問卦] 振興券用質數來命名？")
X
[問卦] 質數的秘密剛發在質數是密碼系統的關鍵 但質數可以排出雙數02468 尾數這五個 因為都可以被二除掉 這一發現![[問卦] 質數的秘密](https://i.imgur.com/qogCfPNb.jpg "[問卦] 質數的秘密")
4
[問卦] 要怎麼數質數？我一個朋友 喜歡數質數 但我數到7 11後就越來越難 每數一個就要檢查他是不是質數 有沒有方法可以有效率的數質數![[問卦] 要怎麼數質數？](https://img.youtube.com/vi/E5vtn_OIe-c/mqdefault.jpg "[問卦] 要怎麼數質數？")
X
[問卦] ..35711以前啊 小學吧 總是要背質數 1 3 5 7 11 13 17 19 … 但是長大後根本沒用到 有沒有數學或者國小學霸能跟我解釋解釋 當初學質數用意在哪？ 該不是為了考試而已吧？
Re: [問卦] 找質數能讓人冷靜下來嗎的卦？2*3*5*7*11*13 + 1 = 30031 = 59*509 你應該是在看質數有無窮多個的證明吧？ -----X
[問卦] 今天3/27來個智力測驗一下今天3/27來個智力測驗一下 1/1、2/4、3/27、4/？ 請問？=多少 答對了 那就是有人類的智力 打錯了 那就和狒狒差不多了
爆
[閒聊] 看了間諜家家酒，覺得約兒很棒![[閒聊] 看了間諜家家酒，覺得約兒很棒](https://i.imgur.com/tDv96plb.jpeg "[閒聊] 看了間諜家家酒，覺得約兒很棒")
爆
[閒聊] 真島浩的年度十大遊戲![[閒聊] 真島浩的年度十大遊戲](https://img.youtube.com/vi/E9EQkWgQZpo/mqdefault.jpg "[閒聊] 真島浩的年度十大遊戲")
89
[問題] 追求畫質 幀數的是少數人嗎![[問題] 追求畫質 幀數的是少數人嗎](https://img.youtube.com/vi/inF-z_Td9YQ/mqdefault.jpg "[問題] 追求畫質 幀數的是少數人嗎")
70
[訃聞] 漫畫家魚夫病逝68
[蔚藍] 甜點貓年末突襲！![[蔚藍] 甜點貓年末突襲！](https://img.youtube.com/vi/mwi08v0BcWk/mqdefault.jpg "[蔚藍] 甜點貓年末突襲！")
57
[妮姬] 抽卡切莫上頭…![[妮姬] 抽卡切莫上頭…](https://i.imgur.com/Ghr6FTdb.jpeg "[妮姬] 抽卡切莫上頭…")
53
Re: [推投] Ave Mujica 最喜歡的成員 催票![Re: [推投] Ave Mujica 最喜歡的成員 催票](https://i.imgur.com/nnpri4vb.jpeg "Re: [推投] Ave Mujica 最喜歡的成員 催票")
爆
[推投] 2024「秋番」最喜歡電視動畫「3票」51
[妮姬] 日服塞爆了![[妮姬] 日服塞爆了](https://i.imgur.com/6DfFhthb.jpeg "[妮姬] 日服塞爆了")
52
[情報] PA Works 新原創 美食渡過每一天![[情報] PA Works 新原創 美食渡過每一天](https://i.imgur.com/OkujKBpb.jpeg "[情報] PA Works 新原創 美食渡過每一天")
42
[死神]朋友:一護在死神中潮度不是前段班,怎反駁?![[死神]朋友:一護在死神中潮度不是前段班,怎反駁?](https://i.imgur.com/ECcrN8tb.jpeg "[死神]朋友:一護在死神中潮度不是前段班,怎反駁?")
54
[問題] 顯卡8G不夠嗎？![[問題] 顯卡8G不夠嗎？](https://i.imgur.com/m6DguBGb.jpeg "[問題] 顯卡8G不夠嗎？")
38
[討論] 王國跟帝國的差異爆
[奶子] 年末的大奶![[奶子] 年末的大奶](https://pbs.twimg.com/media/Gfx9N8WbMAA-3cV.jpg "[奶子] 年末的大奶")
37
[閒聊] B'z 唱現場!!!![[閒聊] B'z 唱現場!!!](https://img.youtube.com/vi/wr7xTGTG-Mo/mqdefault.jpg "[閒聊] B'z 唱現場!!!")
34
[妮姬] 大意了 大家石頭別抽光啊![[妮姬] 大意了 大家石頭別抽光啊](https://i.imgur.com/IbkdQC9b.jpeg "[妮姬] 大意了 大家石頭別抽光啊")
33
[閒聊] 說到「癡心絕對」會想到什麼？![[閒聊] 說到「癡心絕對」會想到什麼？](https://i.imgur.com/41kFGyYb.png "[閒聊] 說到「癡心絕對」會想到什麼？")
19
[閒聊] 台灣色情ACG創作是不是快追上日本了?34
[蔚藍] 哇幹 要被莉央和季榨乾![[蔚藍] 哇幹 要被莉央和季榨乾](https://i.imgur.com/PkmYxOZb.jpeg "[蔚藍] 哇幹 要被莉央和季榨乾")
32
[閒聊] 戀與深空男角雞雞勃起是可以的嗎![[閒聊] 戀與深空男角雞雞勃起是可以的嗎](https://i.imgur.com/WAvChZUb.jpeg "[閒聊] 戀與深空男角雞雞勃起是可以的嗎")
34
[閒聊] FGO是不是真的要島了，全從者輪流PU![[閒聊] FGO是不是真的要島了，全從者輪流PU](https://i.meee.com.tw/DTRGLN0.png "[閒聊] FGO是不是真的要島了，全從者輪流PU")
63
[閒聊] 女兒表現出對角色扮演的高度興趣![[閒聊] 女兒表現出對角色扮演的高度興趣](https://i.imgur.com/zSMqlDmb.png "[閒聊] 女兒表現出對角色扮演的高度興趣")
33
[閒聊] 2.5次元的誘惑 理理沙的人氣怎麼輸那麼慘?![[閒聊] 2.5次元的誘惑 理理沙的人氣怎麼輸那麼慘?](https://i.imgur.com/Uf6R1xOb.jpeg "[閒聊] 2.5次元的誘惑 理理沙的人氣怎麼輸那麼慘?")
30
[閒聊] 為啥妮姬進不去啊![[閒聊] 為啥妮姬進不去啊](https://i.imgur.com/0fOR9lGb.jpeg "[閒聊] 為啥妮姬進不去啊")
60
[閒聊] 魯魯修的三大女主選誰？![[閒聊] 魯魯修的三大女主選誰？](https://i.imgur.com/RY224g3b.jpg "[閒聊] 魯魯修的三大女主選誰？")
29
[蔚藍] 星空最強！![[蔚藍] 星空最強！](https://i.imgur.com/7j90FDOb.jpeg "[蔚藍] 星空最強！")
20
[討論] Asmongold要跌落中國人的神壇了嗎？![[討論] Asmongold要跌落中國人的神壇了嗎？](https://img.youtube.com/vi/H5HYYOHCefo/mqdefault.jpg "[討論] Asmongold要跌落中國人的神壇了嗎？")
28
[閒聊] 瑪車8為什麼現在還這麼能賣啊33
[閒聊] 美國隊長回到過去怎麼受的了?![[閒聊] 美國隊長回到過去怎麼受的了?](https://i.imgur.com/odE62t3b.png "[閒聊] 美國隊長回到過去怎麼受的了?")
22
[FGO] 新年角 五星Saber 獅心王理查![[FGO] 新年角 五星Saber 獅心王理查](https://pbs.twimg.com/media/GgIobxrbwAAdp5o.jpg "[FGO] 新年角 五星Saber 獅心王理查")